編輯：關於Android編程
首先，看一下效果
可能各位在別處看到過類似的東西，我在微信的文章末尾看到有個玩意，感覺有意思，就用代碼實現一下。這篇文章主要把握寫代碼的思路展示一下。
看到上圖，我想各位能想到最簡單的實現方案就是用動畫，切很多圖出來，然後就可以輕松實現了。為了不讓自己再舒適區裡呆的太安逸，就弄點麻煩的：通過計算來實現。文章的末尾會將全部代碼貼出，復制可以直接運行。
重力勢能 E = mgh 動能 E = ?mv2 在理想狀態下，動能和重力式能可以相互轉換，且能量守恆
如果不想太注意細節，以上的知識可以忽略
這步非常簡單，概括來說就是：
相關代碼在文章末尾已經貼出來了（78-121行，代碼中有後續的細節處理，需要甄別下相關的代碼），這裡只是寫下思路，不再重復貼代碼了
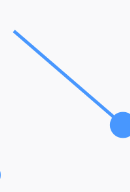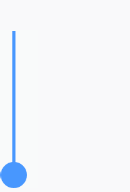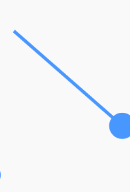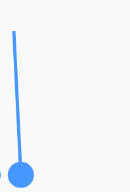
靜態圖為：
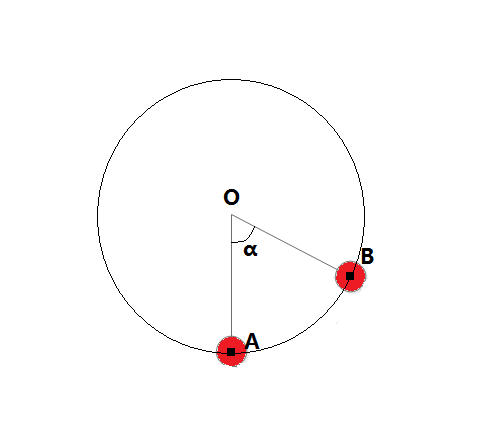
讓帶繩子的球旋轉，實際上就是改變上圖的角α；當α越大，偏移的角度越大；當α越小，偏移的角度越小。
為了讓計算簡單，先假設一些前提：
有了這些前提限制，實際上，每一次繪圖我們的已知條件為：
O點的坐標 大圓的半徑 = 繩子的長度 + 小圓的半徑 α的值（因為前提中的2和3，繪制的時候是可以知道當前α的角度）所以，這步的大致流程為：
根據大圓的圓心O、半徑R，當前α的角度，求B點的坐標（跟前一篇類似，通過畫弧，再通過PathMeasure.getPosTan()來獲得相應點的坐標） 繪制線段OB 以B點為圓心，畫半徑為固定值的小圓相關代碼在文章末尾已經貼出來了（128-212行，代碼中有後續的細節處理，需要甄別下相關的代碼），這裡只是寫下思路，不再重復貼代碼了
如果第一步不知道如何去測量B點的坐標，建議先去看下我前兩篇的文章
音量調節
繪制儀表盤
在上一步中，我們為了簡化模型，讓α的改變量每次都為1，但是，這與現實不相符。現實情況是這樣的：
球偏移到最高點時，速度很慢，基本上為0 球偏移到最低點，速度最快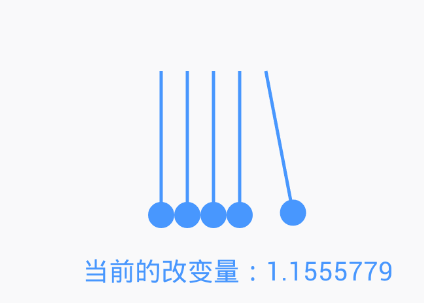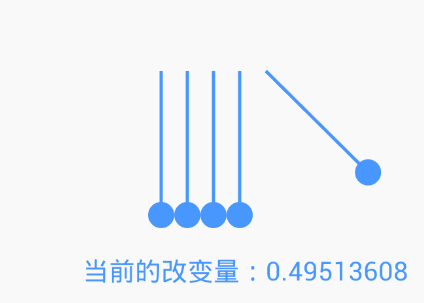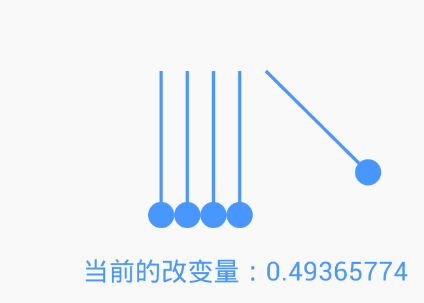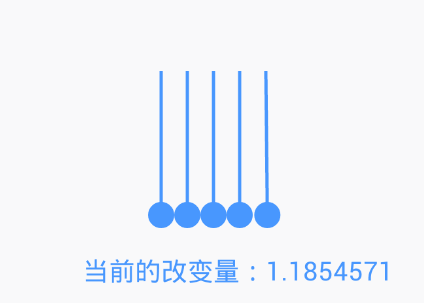
文章一開始，我們已經准備好了需要回憶的知識，現在，讓我們回到物理學課堂，說一說簡單的擺鐘模型計算：
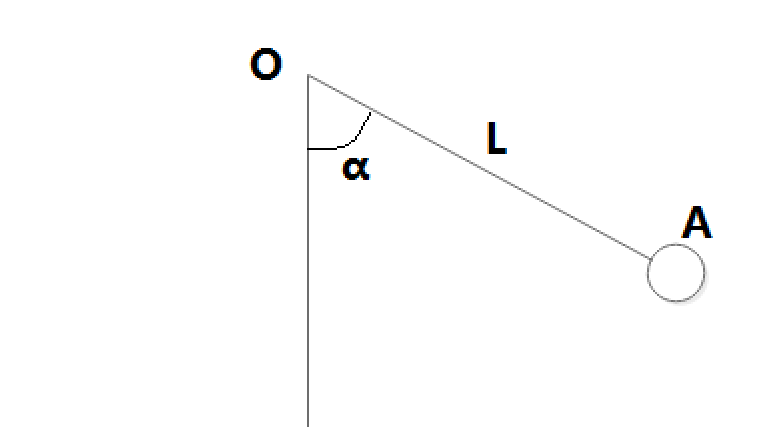
條件：繩子的長為L，球A靜止時，豎直方向的夾角為α
求：當與豎直方向的夾角為β時的角速度
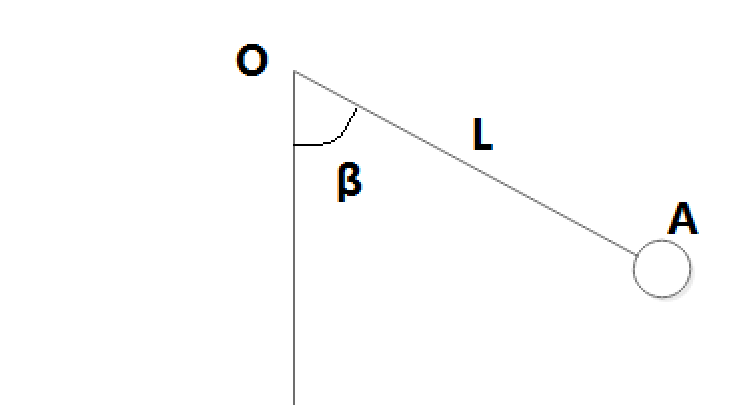
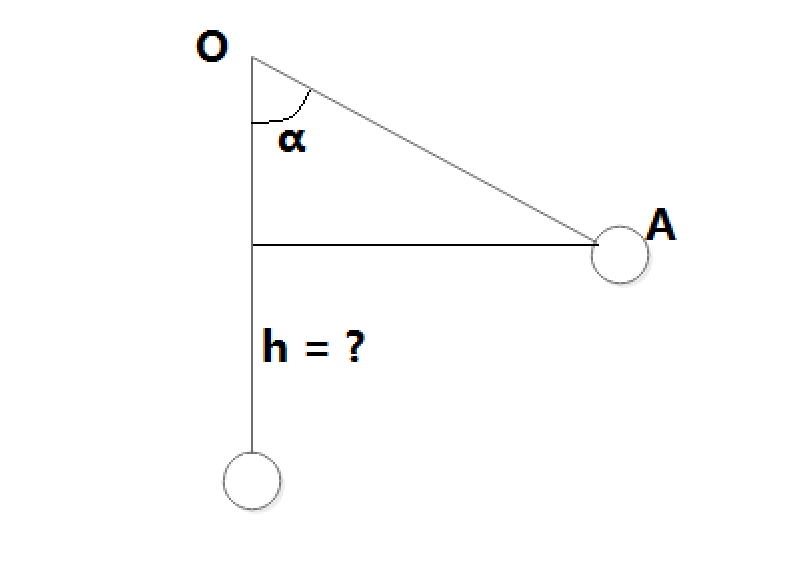
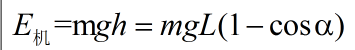一般情況的表示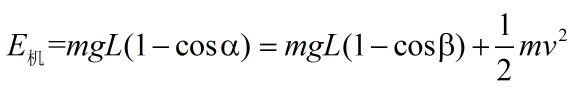
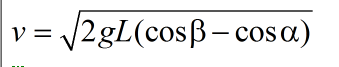
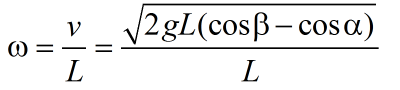
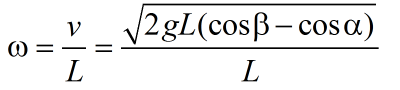
好了，得出了結論，讓我們回到代碼中來：
//計算當前的速率 float v = (float) Math.sqrt(2 * 9.8 * L * (Math.cos( β* Math.PI / 180) - cos(α* Math.PI / 180))); //計算角速度 float w = v / L;
說明：這裡只是擬合，並沒有特別精確。我們認為當前角度到改變後的角度之間的角速度是一致的，都為當前角度所對應的角速度；所以，在當前角度下，改變角度的量為：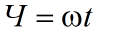
具體的實現過程在下面代碼的219-225行，是不是感覺很簡單？
上面羅裡吧嗦的半天，終於給出來了可以復制的東西 O(∩_∩)O~
/**
* Created by kevin on 2016/9/2.
* <p>
* 需要推敲的地方：
* 1.並排繪制多個帶繩子的球
* 2.讓左右兩端的球可以旋轉
* 3.為了模擬現實，需要根據物理學來計算單位時間旋轉的角度
*/
public class Pendulum extends View {
private Paint linePaint;
private int width;
private int height;
private Path linePath;//用來繪制靜態部分的Path
private Path bigCirclePath;//用來測量大圓的Path
private Path rotateLinePath;//用來繪制動態部分的Path
private int stroke = 5; //線段的寬度
private int r = 20; //圓圈的半徑
private int length = 200; //線的長度
private int number = 5; //球的個數（奇數，偶數感覺丑就沒實現）
private static int angle = 50;//最大旋轉角度
// 第一個參數表示角度；負數表示左邊球旋轉的角度，正數表示右邊球旋轉的角度
// +angle表示右側球偏離最大的角度為30度
// -angle表示左側球偏離最大的角度為30度
// 第二個參數表示方向；-1表示從右往左擺動，1表示從左往右擺動
private float[] degree = new float[]{angle, -1};
private float t = 2f;//時間；可以用來控制速率，t越小，擺鐘越慢；t越大，擺鐘越快
private float cosO;//cosθ,是個固定值
private float gr2;//2gr，是個固定值
public Pendulum(Context context) {
super(context);
initPaint();
calCosOAnd2gr();
}
public Pendulum(Context context, AttributeSet attrs) {
super(context, attrs);
initPaint();
calCosOAnd2gr();
}
public Pendulum(Context context, AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
initPaint();
calCosOAnd2gr();
}
/**
* 用來計算cosθ和2gr
*/
private void calCosOAnd2gr() {
//這裡為了避免cosα-cosθ=0的情況，所以+0.1
cosO = (float) Math.cos((angle + 0.1f) * Math.PI / 180);
//2倍的重力加速度乘以半徑
gr2 = (float) (9.8 * r * 2);
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
canvas.translate(width / 2, height / 2);
drawPic(canvas);
rotate(canvas);
}
/**
* 繪制靜態圖形
*
* @param canvas
*/
private void drawPic(Canvas canvas) {
if (number < 1) {
throw new IllegalArgumentException("數量不能小於1");
}
int x;
if (number % 2 == 1) {
//奇數的情況
//用來確定最外層的位置，例如：如果number為3，leftNumber為1
// number為5，leftNumber為2
// number為7，leftNumber為3
int leftNumber = number / 2;
for (int i = -leftNumber; i <= leftNumber; i++) {
if (isRight()) {
//最右側在搖擺
if (i == leftNumber)
continue;
} else if (!isRight()) {
//最左側的在搖擺
if (i == -leftNumber)
continue;
}
//計算圓心的橫坐標x
x = 2 * r * i;
if (linePath == null)
linePath = new Path();
linePath.reset();
//move到圓心(更准確的坐標為(x,-r),圓繪制出來會把部分線段覆蓋；這裡只是為了方便表示，不再增加多余的點)
linePath.moveTo(x, 0);
//畫直線到頂點，（頂點離圓心= 線段的長度 + 半徑）
linePath.lineTo(x, -(r + length));
//繪制直線
linePaint.setStyle(Paint.Style.FILL_AND_STROKE);
canvas.drawPath(linePath, linePaint);
//繪制圓圈，為了不重合，使用FILL，不繪制線的寬度
linePaint.setStyle(Paint.Style.FILL);
canvas.drawCircle(x, 0, r, linePaint);
}
} else if (number % 2 == 0) {
//偶數
throw new IllegalArgumentException("偶數太丑，沒有繪制");
}
}
/**
* 繪制旋轉的圖形
*
* @param canvas
*/
private void rotate(Canvas canvas) {
//左側球運動和右側球運動是對稱的，使用direction（值為+1或-1）來做標記
int direction;
if (isRight()) {
//右側球運動，+1
direction = 1;
} else {
//左側球於東，-1
direction = -1;
}
//measure.getPosTan()中不接受負數，這裡需要取絕對值
float nowDegree = Math.abs(degree[0]);
linePaint.setStyle(Paint.Style.STROKE);
//確定單側外層圖片的個數
int pointNumber = number / 2;
//確定靜態圓形的橫坐標，與drawPic中的（x = 2 * r * i）相似
int x = 2 * r * pointNumber * direction;
//用來確定大圓圓心的坐標，同時也是線段頂點的坐標
float[] topPoint = new float[]{x, -(r + length)};
int totalLength = length + r;
if (bigCirclePath == null)
bigCirclePath = new Path();
bigCirclePath.reset();
//rectF是用來繪制弧形的：以線段的頂點為圓心，length + r為半徑畫弧形
RectF rectF = new RectF(topPoint[0] - totalLength, topPoint[1] - totalLength, topPoint[0] + totalLength, topPoint[1] + totalLength);
//繪制1/4個圓的弧形
bigCirclePath.addArc(rectF, 90, -90 * direction);
//用來確定旋轉nowDegree時的邊界坐標；
float[] rotatePoint = new float[2];
PathMeasure measure = new PathMeasure(bigCirclePath, false);
//此時，rotatePoint的坐標就為我們圖中小圓圈圓心的坐標
measure.getPosTan(measure.getLength() * (nowDegree) / 90, rotatePoint, null);
//到現在為止，我們已經知道了圓心的坐標以及線段頂點的坐標了。
//下面，我們就鏈接這個兩個點，並以rotatePoint為圓心畫圓
//畫線段
if (rotateLinePath == null)
rotateLinePath = new Path();
rotateLinePath.reset();
rotateLinePath.moveTo(topPoint[0], topPoint[1]);
rotateLinePath.lineTo(rotatePoint[0], rotatePoint[1]);
canvas.drawPath(rotateLinePath, linePaint);
//畫圓
linePaint.setStyle(Paint.Style.FILL);
canvas.drawCircle(rotatePoint[0], rotatePoint[1], r, linePaint);
//顯示文字用的，不用理會
linePaint.setTextSize(40);
canvas.drawText("偏移的角度：" + degree[0] + "", -100, 100, linePaint);
//degree[1]表示方向，當為1時，表示從左向右運動，那麼degree[0]需要不斷增加（這是我規定的；當然要修改的話，可以根據情況來修改，估計修改時會暈菜一段時間）
if (degree[1] == 1) {
//從總往右,degree增大
if (degree[0] < angle) {
//計算需要轉動的角度
float changeAngle = rotateAngle();
//改變當前角度的值
degree[0] = degree[0] + changeAngle;
invalidate();
}
//當達到最右側時，方向翻轉
if (degree[0] >= angle) {
degree[1] = -1;
}
}
//degree[1]表示方向，當為-1時，表示從右向左運動，那麼degree[0]需要不斷減小（這是我規定的；當然要修改的話，可以根據情況來修改，估計修改時會暈菜一段時間）
else if (degree[1] == -1) {
//從右往左，degree減小
if (degree[0] > -angle) {
//計算需要轉動的角度
float changeAngle = rotateAngle();
//改變當前角度的值
degree[0] = degree[0] - changeAngle;
invalidate();
}
//當達到最左側時，方向翻轉
if (degree[0] <= -angle) {
degree[1] = 1;
}
}
}
/**
* 計算當前需要轉動的角度
*
* @return
*/
private float rotateAngle() {
//計算當前的速率
float v = (float) Math.sqrt(gr2 * (Math.cos(Math.abs(degree[0]) * Math.PI / 180) - cosO));
//計算需要改變的弧度
float changedAngle = t * v / r;
return changedAngle;
}
/**
* 判斷是否是右側的圓球在動
*
* @return true-->右側的圓球在動
* false-->左側的圓球在動
*/
private boolean isRight() {
boolean flag = false;
//degree[0]大於0，表示右側球在動
//degree[1]小於0，表示左側球在動
if (degree[0] > 0) {
flag = true;
} else if (degree[0] < 0) {
flag = false;
} else if (degree[0] == 0) {
//如果degree等於0，需要根據方向來判斷哪個求在動
//degree[1]等於-1表示：球是從右往左在運動，此時，球的速度 v-->0，但還是右側的球在動
if (degree[1] == -1) {
flag = true;
}
//與上面的情況相反，是左側的球在動
else if (degree[1] == 1) {
flag = false;
}
}
return flag;
}
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
width = w;
height = h;
}
private void initPaint() {
//這裡不想弄多個Paint,就用一個Paint來替代了，如果有需要，可以增加Paint來繪制指定的圖形
linePaint = new Paint();
linePaint.setStrokeWidth(stroke);
linePaint.setAntiAlias(true);
linePaint.setStyle(Paint.Style.FILL_AND_STROKE);
linePaint.setColor(0xff4897fe);
}
}</p>
用些簡單的物理學知識，感覺好奇怪，不過還好，物理學翻譯成代碼也只有3行而已。
Android ExpandableListView的使用
ExpandableListView可擴展列表一般可用來開發類似QQ聯系人的界面效果。簡單整理了一下ExpandableListView的使用，希望幫助到需要的親們，由於
安裝Android Studio相關教程分析
安裝Android Studio相關教程（不翻牆版）這篇文章是當年自己剛用android studio時寫的，主要是當時同班同學問題太多，後來我直接寫了這篇。現在發上來給
詳解Android中Service服務的基礎知識及編寫方法
首先，讓我們確認下什麼是service？ service就是android系統中的服務
Android中的各種保活1
目前市面上的應用，貌似除了微信和手Q都會比較擔心被用戶或者系統（廠商）殺死問題。本文對 Android 進程拉活進行一個總結。Android 進程拉活包括兩個層面：A.
